Welcome to the Center for Subsurface Energy and the Environment

Webinar with Ryosuke Okuno
Aqueous Nanobubble Dispersion for Geologic Carbon Sequestration and Enhanced Oil Recovery
Tuesday, May 14, 2024, Noon Central
Read more
Industrial Affiliate Programs Spotlight
Energi Simulation IAP on Carbon Utilization and Storage
Learn More
Home
Featured Research Topic
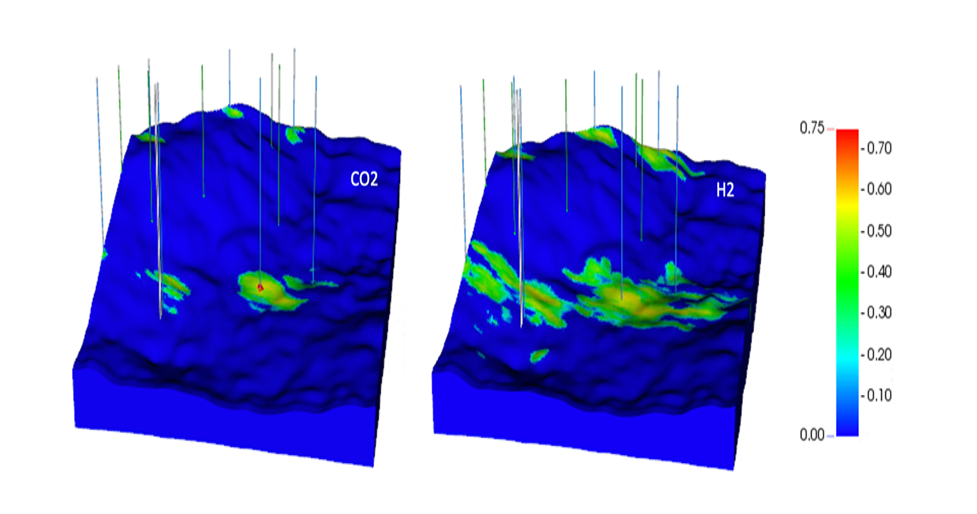
Hydrogen Storage may become an important factor as we transition to low-carbon energy sources. Because hydrogen combustion produces no CO2, and energy demand fluctuates on a seasonal basis, it can be advantageous to store hydrogen to be used when it is needed.
Learn More
Image details: Gas saturations after 3 years of CO2 injection (a) and hydrogen injection (b).
Research Highlights
-
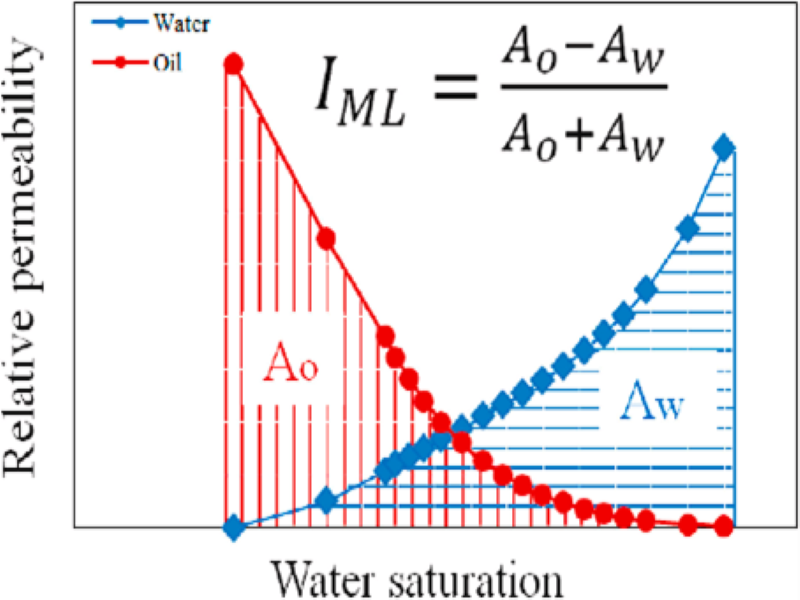 Recent applications of relative permeability data: ‘wettability evaluation’ and ‘dynamic rock typing’ – Abouzar Mirzaei Paiaman
Recent applications of relative permeability data: ‘wettability evaluation’ and ‘dynamic rock typing’ – Abouzar Mirzaei Paiaman
We present this research in two parts.
-
 Glass Microfluidics for Carbonates Dissolution and Precipitation - Jianping Xu
Glass Microfluidics for Carbonates Dissolution and Precipitation - Jianping Xu
The dissolution and precipitation of carbonates are critically important processes in a wide array of...
-
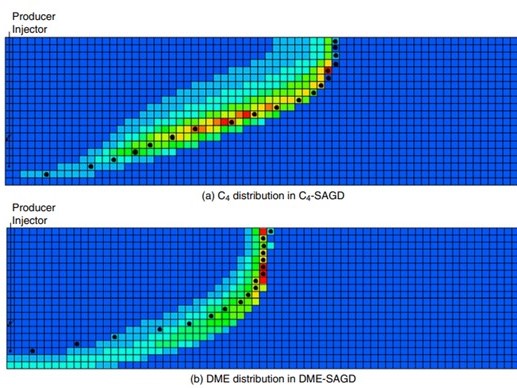 Novel solvents for energy-efficient enhanced oil recovery - Kai Sheng
Novel solvents for energy-efficient enhanced oil recovery - Kai Sheng
Novel solvent, such as Dimethyl Ether (DME), can be used as a solvent aid for thermal EOR...
Resources
Events
Effect of CO2 Injection on the Poromechanical and Multiphase Flow Characteristics of Subsurface Rock
Kiseok Kim, Ph.D. , Assistant Professor, Harold Vance Department of Petroleum Engineering, Texas A&M University
Friday, April 26, 2024, 9:00am - 10:00 am CST
Bureau Seminar Series
Webinar with Ryosuke Okuno
Aqueous Nanobubble Dispersion for Geologic Carbon Sequestration and Enhanced Oil Recovery
May 14, 2024, Noon Central
CSEE Webinar
CSEE News
UT PGE/CSEE Awarded First-Ever DOE Funding for Geologic H2 Research
Four Hildebrand Department of Petroleum and Geosystems Engineering and Center for Subsurface Energy and the Environment faculty members received funding from the U.S. Department of Energy Advanced Research Projects Agency–Energy (ARPA-E) in February as part of a $20 million effort to accelerate the natural subsurface generation of low-cost, low-emissions hydrogen. This is the first time that the U.S. government has competitively selected teams to research this kind of technology.
Professor Quoc Nguyen receives the 2023 WesTEC Distinguished Leader in Science and Technology Award
WesTEC is the Canada Operations Technical Excellence Conference hosted by Dow Chemical and The Royal Society of Chemistry for over 30 years. The WesTEC award recognizes technical innovation, and technology breakthroughs. Quoc’s breakthrough work in developing innovative solutions for conformance control, unconventional EOR, and flow assurance from lab to field made him a well-deserved recipient of this prestigious award.
Research Professor Mojdeh Delshad has been awarded the 2024 SPE IOR Pioneer Award
Dr. Delshad of CSEE and the Hildebrand Department of Petroleum and Geosystems Engineering will receive the award at the SPE IOR meeting in Tulsa in April, 2024.
The SPE IOR Pioneer Award ( http://speior.org/pioneer-award/ ) is presented to selected individuals who have made significant advancements over the years in improved oil recovery technology. This award has been presented to 90 individuals since its inauguration in 1984.
Professor Larry Lake Announces Retirement
Professor Larry W. Lake of CSEE and Hildebrand Department of Petroleum and Geosystems Engineering is retiring after four decades. Dr. Lake will be slowly scaling back his teaching load over the next three years.
Associate Professors Espinoza and Livescu Awarded $5 Million ARPA-E Grant
CSEE and Hildebrand Department of Petroleum and Geosystems Engineering (UT PGE) Associate Professors Nicolas Espinoza and Silviu Livescu are key team members of a new $5 million grant from the Mining Innovations for Negative Emissions Resource Recovery (MINER) program run by the U.S. Department of Energy’s (DOE) Advanced Research Projects Agency–Energy (ARPA-E).
Associate Professor Zoya Heidari is the Recipient of the 2023 SPE International Formation Evaluation Award
The Formation Evaluation Award of the Society of Petroleum Engineers recognizes outstanding achievement or contributions to the advancement of petroleum engineering in the area of formation evaluation.
Professor Kishore Mohanty to serve as Interim Director of CSEE effective July 15
He will serve in this role until the next director is appointed. Dr. Mohanty served as Director from 2014 to 2020.
Associate Professor David DiCarlo named a UT Accesibility Champion
A UT Accesibility Champion has demonstrated his/her commitment to fostering an accessible, inclusive, and welcoming campus for students with disabilities.